Бином Ньютона
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
(a + b)n = an + C1n an - 1 b + C2n an - 2 b2 +...+Ckn an - k bk +... + Cn - 1n abn - 1 + Cnnbn
или
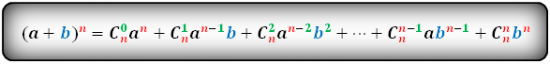
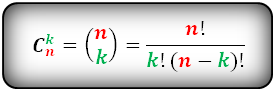
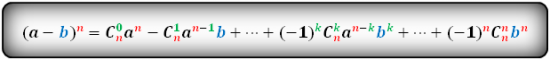
Разложения бинома Ньютона для первых значений n.
(a + b)0= 1
(a + b)1= a+ b
(a + b)2= a2 + 2ab + b2,
(a + b)3= a3 + 3a2b + 3ab2 + b3,
(a + b)4= a4 + 4a3b + 6a2b2 + 4ab3 + b4,
(a + b)5= a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5,
(a + b)6= a6+6a5b + 15a4b2+20a3b3 + 15a2b4+6ab5+b6.
Запишем так:
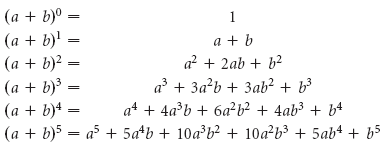
Треугольник Паскаля.
Для того чтобы облегчить труд школяров и студентов, великий французский математик и физик Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент для определения этих самых коэффициентов — «треугольник Паскаля».
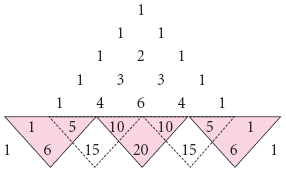
Бином Ньютона с использованием треугольника Паскаля
Для (a + b)8, мы дополняем две строки к треугольнику:
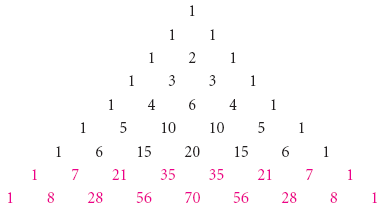
Тогда (a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Обобщим наши результаты следующим образом.
Для любого бинома a+ b и любого натурального числа n,
(a + b)n = c0anb0 + c1an-1b1 + c2an-2b2 + .... + cn-1a1bn-1 + cna0bn, где числа c0, c1, c2,...., cn-1, cn взяты с (n + 1) ряда треугольника Паскаля.
Сочетания.
Комбинации из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом, называются сочетаниями и обозначаются:
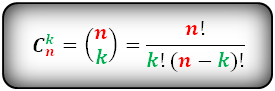
Пример 1 Сколькими способами можно распределить три путевки в санаторий между пятью желающими?
Ответ: 10.
Пример 2 В цехе работают 12 человек: 5 женщин и 7 мужчин. Сколькими способами можно сформировать бригаду из 7 человек, чтобы в ней было 3 женщины?
Ответ: 350
Примеры решения задач с использованием Бинома.
